分形与混沌(Chapter 1)
分形概述
分形(英语:fractal,源自拉丁语:frāctus,有“零碎”、“破裂”之意),又称碎形、残形,通常被定义为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都(至少近似地)是整体缩小后的形状”即具有自相似的性质。
分形在数学中是一种抽象的物体,用于描述自然界中存在的事物。而人工实现的分形通常在放大后能展现出相似的形状,因此分形也被称为扩展对称或展开对称。如果在每次放缩(递归)后,图形形状的重复是完全相同的,这就被称为自相似。自相似的典型例子如门格海绵:
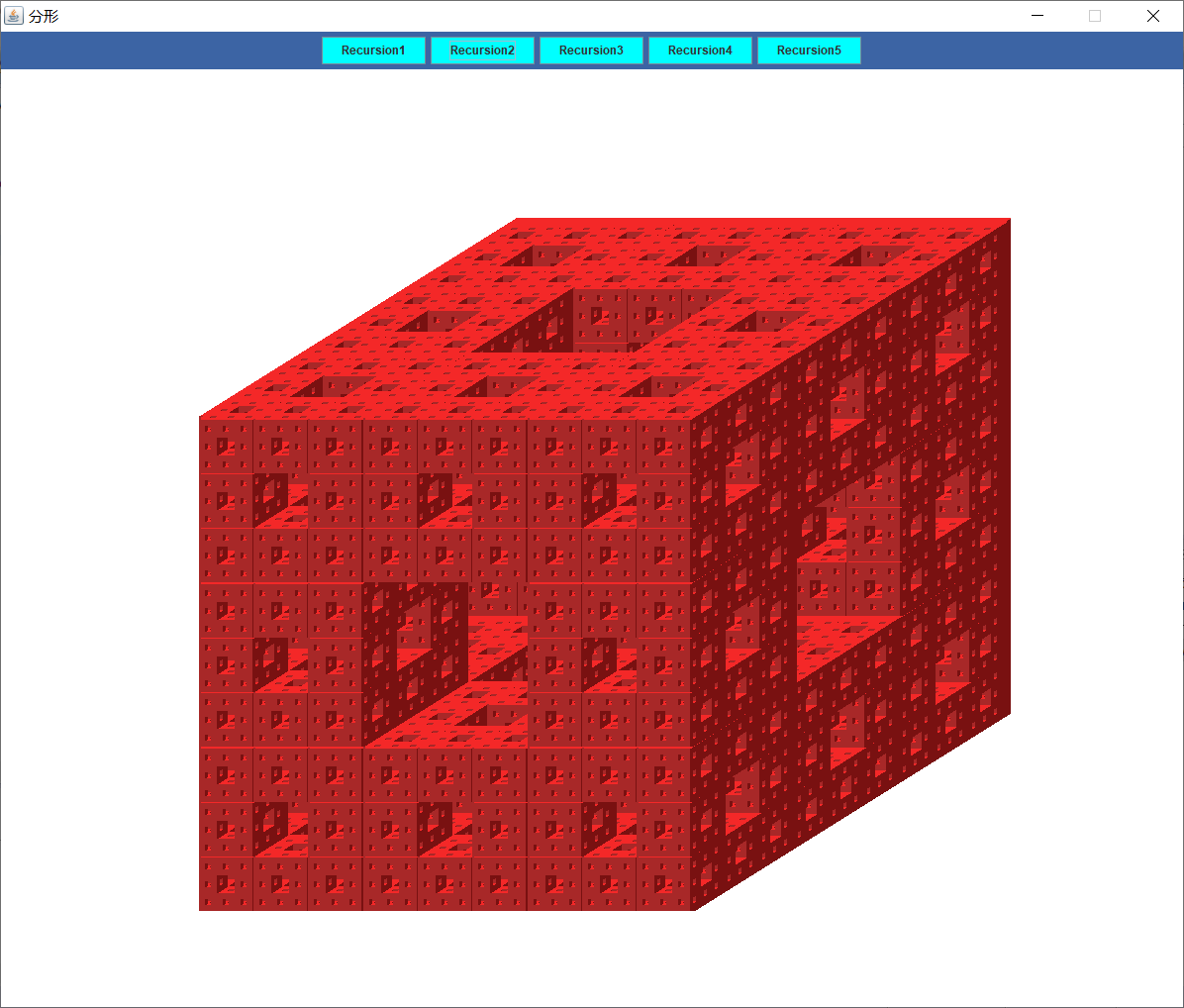
如图所示,这就是一个递归了5次的 门格海绵,它的每一个单元都是自相似的。
分形图像自身细节的重复意味分形与其他几何图形相似但又有所不同。当你放缩一个图形时,你就能看出分形和其他几何图形的区别:
如果将分形的一维长度加倍,分型空间填充变为 2的n次方 倍,但此时n 不一定是个整数,指数 n 称为分型的维数。
作为一个数学函数,分形通常是处处不可微的。无穷分形曲线可以理解为一条一维的曲线在空间中绕行,它的拓扑维数仍然是 1,但大于 1 的分形维数暗示了它有着类似曲面的性质。
总之,分形作为一个重要的数学分支,从17世纪被提出至今,有着庞大而复杂的学术体系与应用方向,这里不再赘述。感兴趣的读者可以去维基百科自行查阅。
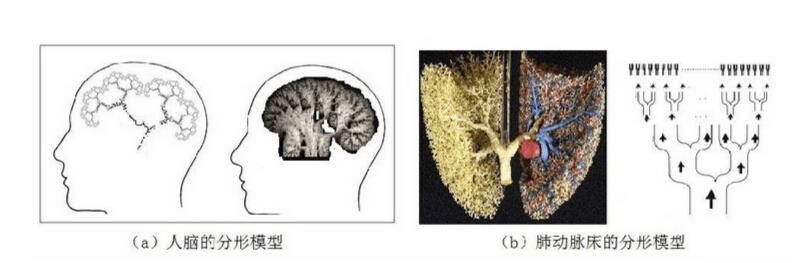
分形——解构世界的算法
如图所示,根据分形原理,如果将一棵树的树杈不断缩放,去观察局部,那么自相似的性质就非常明显了。


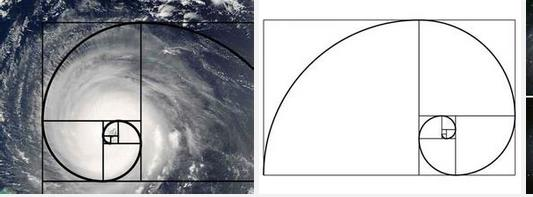
再比如说斐波那契螺旋线分形:


混沌之谜–逻辑斯蒂方程
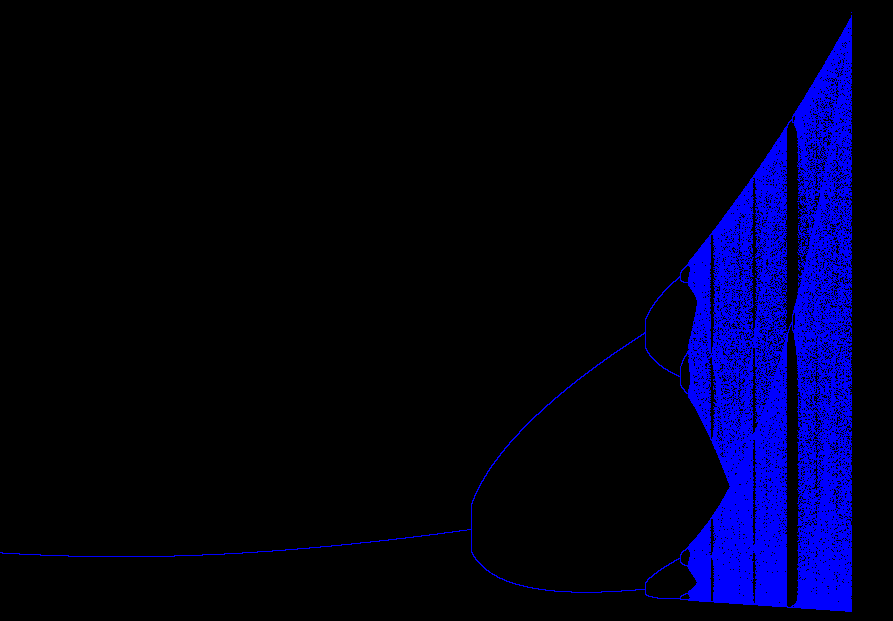
分形举例
噪声:

多面体:
帕斯卡三角形 & 塞尔宾斯基堆

塞尔宾斯基地毯
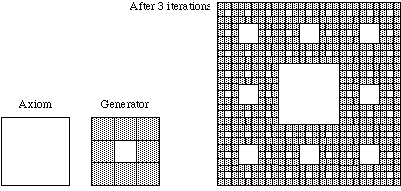
除此之外还有门格海绵、开普勒多面体等。
IFS分形

还有类似于上文的 枫叶 也属于IFS分形。
L-系统
这个类型的分形常用来实现类似上文中植物的分形。这里因为篇幅不再举例。
结语
分形的种类繁多,瑰丽而奇异。这其中蕴含这无数数学家与程序员的智慧。笔者才疏学浅,即使绞尽脑汁,也仅能勘知一二。一个分形体既可以仅仅是一条1.26维的线段,也可以是绚丽的3D效果(如光线追踪)。本篇博客简单介绍了分形的一些概念即其种类,笔者会在接下来的博客中详细介绍用Java语言实现几种简单分形体的具体方法,不定期更新,敬请关注哦。
